2021年普通高等学校招生全国统一考试
数学
本试卷共4页,22小题,满分150分。考试用时120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。将条形码横贴在答题卡右上角“条形码粘贴处”。
2.作答选择题时,选出每小题答案后,用2B铅笔在答题卡上对应题目选项的答案信息点涂黑:如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保持答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合
![]()
![]()
![]()
A.
![]()
![]()
![]()
![]()
2.已知
![]()
![]()
A.
![]()
![]()
![]()
![]()
3.已知圆锥的底面半径为
![]()
A.2 B.
![]()
![]()
4.下列区间中,函数
![]()
A.
![]()
![]()
![]()
![]()
5.已知
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A.13 B.12 C.9 D.6
6.若
![]()
![]()
A.
![]()
![]()
![]()
![]()
7.若过点
![]()
![]()
A.
![]()
![]()
![]()
![]()
8.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球,甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则()
A.甲与丙相互独立B.甲与丁相互独立
C.乙与丙相互独立D.丙与丁相互独立
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.有一组样本数据
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样数据的样本极差相同
10.已知
![]()
![]()
![]()
![]()
![]()
A.
![]()
![]()
C.
![]()
![]()
11.已知点
![]()
![]()
![]()
![]()
A.点
![]()
![]()
B.点
![]()
![]()
C.当
![]()
![]()
D.当
![]()
![]()
12.在正三棱柱
![]()
![]()
![]()
![]()
![]()
![]()
A.当
![]()
![]()
B.当
![]()
![]()
C.当
![]()
![]()
![]()
D.当
![]()
![]()
![]()
![]()
三、填空题:本题共4小题,每小题5分,共20分。
13.已知函数
![]()
![]()
14.已知
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
15.函数
![]()
16.某校学生在研究民间剪纸艺术时,发现剪纸时经常会沿纸的某条对称轴把纸对折.规格为
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
已知数列
![]()
![]()
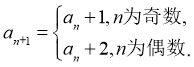
(1)记
![]()
![]()
![]()
![]()
(2)求
![]()
18.(12分)
某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B类问题中的每个问题回答正确得80分,否则得0分.
己知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.
(1)若小明先回答A类问题,记
![]()
![]()
(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.
19.(12分)
记
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(1)证明:
![]()
(2)若
![]()
![]()
20.(12分)
如图,在三棱锥
![]()
![]()
![]()
![]()
![]()
![]()
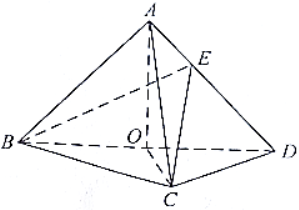
(1)证明:
![]()
(2)若
![]()
![]()
![]()
![]()
![]()
![]()
![]()
21.(12分)
在平面直角坐标系
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(1)求
![]()
(2)设点
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
22.(12分)
已知函数
![]()
(1)讨论
![]()
(2)设
![]()
![]()
![]()
![]()
扫码关注学科网数学服务号,第一时间获取2021年高考真题、答案、解析