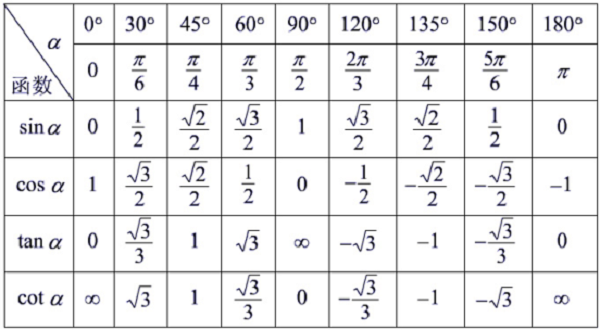
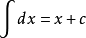sinx的导数是cosx,而cosx的导数是 -sinx,这是因为两个函数的不同的单调区间造成的。函数可导的条件:如果一个函数的定义域为全体实数,即函数在其上都有定义。
什么是sin函数
sinx函数,即正弦函数,三角函数的一种。正弦函数是三角函数的一种。对于任意一个实数x都对应着唯一的角(弧度制中等于这个实数),而这个角又对应着唯一确定的正弦值sinx,这样,对于任意一个实数x都有唯一确定的值sinx与它对应,按照这个对应法则所建立的函数,表示为y=sinx,叫做正弦函数。
锐角正弦函数
在直角三角形ABC中,∠C是直角,AB是∠c斜边,BC是∠A的对边,AC是∠B的对边。
正弦函数就是sin(A)=BC/AB
sinA=∠A的对边:斜边
sinx的导数是cosx(其中x为变量),sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是-sinX,这是因为两个函数的不同的升降区间造成的。
sinx导数推导过程
(sinx)'=lim[sin(x+△x)-sinx]/(△x),其中△x→0,
将sin(x+△x)-sinx展开,
sinxcos△x+cosxsin△x-sinx,由于△x→0,故cos△x→1,
从而sinxcos△x+cosxsin△x-sinx→cosxsin△x,
于是(sinx)’=lim(cosxsin△x)/△x,
△x→0时,lim(sin△x)/△x=1
所以
(sinx)’=cosx