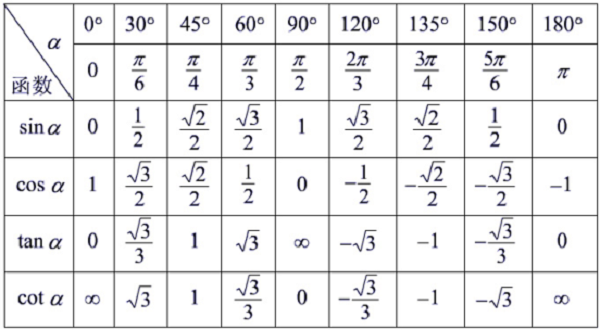
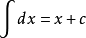意义不同、含义不同、包含范围不同、定义不同。无穷大的观察背景是过程,无界变量的判断前提是区间。无穷小和无穷大量的名称中隐含着它们(在特定过程中)的发展趋势;而无界变量的意思是,在某个区间内,其绝对值没有上界。
无界变量和无穷大量的区别
在适当选定的区间内,无穷大可以是无界变量。
无穷大:如果对于任意给定的正数M,都存在δ>0(或正数X),使当0<|x-x0 |<δ<(或|x|>X)时,“恒有”|f(x)| > M,则称f(x)是x→x0(或x—∞)时的“无穷大量”。
无界变量:如果对于任意给定的正数M,都存在函数定义域中的一点x*,使|f(x*)|≥M,则称,f(x)是“无界变量”。
无界变量为什么不一定是无穷大量
因为变量的大小在无穷循环。
无界函数的概念是指某个区间上的。若对于任意的正数m,总存在某个点,使得|f(x)|>m,则称该函数是区间上的无界函数。
无穷大量是指在自变量的某个趋限过程(例)下因变量的变化趋势。若自变量x无限接近x0(或|x|无限增大)时,函数值|f(x)|无限增大,则称f(x)为x→x0(或x→无穷)时的无穷大量。例如f(x)=1/(x-1)2是当x→1时的无穷大量,f(n)=n2是当n→∞时的无穷大量。