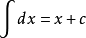基本导数公式(y:原函数;y':导函数):1、y=c,y'=0(c为常数)。2、y=x^μ,y'=μx^(μ-1)(μ为常数且μ≠0)。3、y=a^x,y'=a^x lna;y=e^x,y'=e^x。4、y=logax,y'=1/(xlna)(a>0且a≠1);y=lnx,y'=1/x等。
求导公式有哪些
c'=0(c为常数)
(x^a)'=ax^(a-1),a为常数且a≠0
(a^x)'=a^xlna
(e^x)'=e^x
(logax)'=1/(xlna),a>0且 a≠1
(lnx)'=1/x
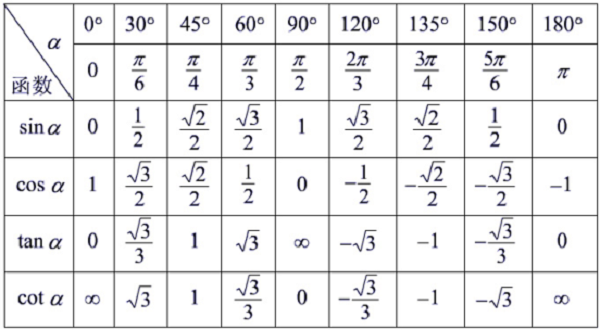
(sinx)'=cosx
(cosx)'=-sinx
(tanx)'=(secx)^2
(secx)'=secxtanx
(cotx)'=-(cscx)^2
(cscx)'=-csxcotx
(arcsinx)'=1/√(1-x^2)
(arccosx)'=-1/√(1-x^2)
(arctanx)'=1/(1+x^2)
(arccotx)'=-1/(1+x^2)
(shx)'=chx
(chx)'=shx
(uv)'=uv'+u'v
(u+v)'=u'+v'
(u/)'=(u'v-uv')/^2
导数基本公式整理
1.y=c(c为常数) y'=0
2.y=x^n y'=nx^(n-1)
3.y=a^x y'=a^xlna
4.y=logax y'=logae/x
5.y=sinx y'=cosx
6.y=cosx y'=-sinx
7.y=tanx y'=1/cos^2x
8.y=cotx y'=-1/sin^2x
9.y=e^x y'=e^x
10.y=lnx y'=1/x
导数的基本性质:
(1)若导数大于零,则单调递增;若导数小于零,则单调递减;导数等于零为函数驻点,不一定为极值点。需代入驻点左右两边的数值求导数正负判断单调性。
(2)若已知函数为递增函数,则导数大于等于零;若已知函数为递减函数,则导数小于等于零。
(3)可导函数的凹凸性与其导数的单调性有关。如果函数的导函数在某个区间上单调递增,那么这个区间上函数是向下凹的,反之则是向上凸的。如果二阶导函数存在,也可以用它的正负性判断,如果在某个区间上恒大于零,则这个区间上函数是向下凹的,反之这个区间上函数是向上凸的。曲线的凹凸分界点称为曲线的拐点。