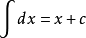可逆矩阵一定是方阵。可逆矩阵最终一定可以化为E的形式,如果可逆矩阵不是方阵那么怎么可能化为E的形式,所以可逆矩阵一定是方阵。如果一个矩阵不是方阵,是不存在逆矩阵的,如果对其求逆,就是求它的伪逆,可以通过程序实现。
可逆矩阵是方阵吗
比如一个2*3的矩阵,它的伪逆矩阵就是一个3*2的矩阵,两者相乘之后得到2*2的单位矩阵。
对于一般性的矩阵(一般的矩阵,行数不一定等于列数),有行满秩和列满秩两个概念。当然对于方阵,行数=列数,所以就不必分行满秩和列满秩,就是满秩了。
可逆矩阵只是针对方阵而言的,不是方阵的矩阵,不存在可逆或不可逆的概念。只有方阵才能说可逆方阵和不可逆方阵。
可逆矩阵是什么意思:
矩阵可逆是指一个矩阵拥有对应逆矩阵的情况。
可逆矩阵是线性代数中的一个矩阵,其定义为在线性代数中,给定一个 n 阶方阵A,若存在一n 阶方阵B,使得AB=BA=In(或AB=In、BA=In 任满足一个),其中In 为n 阶单位矩阵,则称A 是可逆的,且B 是A 的逆阵,记作 A^(-1)。
方阵和矩阵的区别是什么
方阵和矩阵的区别是形式不同。
1.方阵实际上是一种特殊的矩阵,当矩阵的行数和列数目相等时,可以称之为方阵,比如:某一矩阵的行与列数都是5,可以称之为5阶方阵。
2.二个矩阵相加就是将每一行元素加起来,两行列式相加,使操作的结果相加,在一些特殊的情况下(如行或列),只能将一行(或列)元素相加,其余元素照写。
3.在线性空间中矩阵是一个元素。行列式是矩阵的一种性质。近代数学中行列式的概念已被边缘化,行列式在实际应用中可以说只是一个矩阵的计算而得很有用。