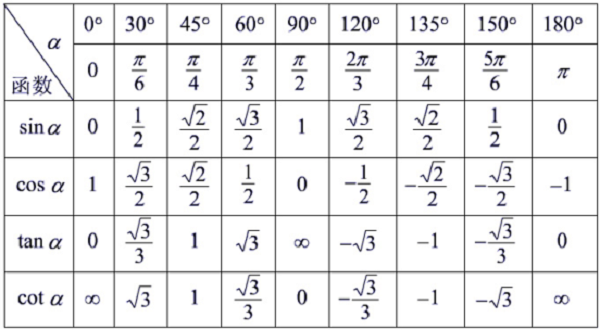
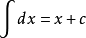卡方分布的自由度为n-k。卡方分布的自由度取决于总体参数的个数,一般来说,自由度等于总体参数的个数减去一。例如,如果总体有三个参数,那么卡方分布的自由度就是2。
卡方分布的自由度怎么确定
一个式子中独立变量的个数称为这个式子的“自由度”,确定一个式子自由度的方法是:若式子包含有n个独立的随机变量,和由它们所构成的k个样本统计量,则这个表达式的自由度为n-k。比如中包含ξ1,ξ2,…,ξn这n个独立的随机变量,同时还有它们的平均数ξ这一统计量,因此自由度为n-1。
证明:设k1ξ1+k2ξ2+…+knξn=0.这是一个含有n个相对独立变量的式子。则其中任意一个ξi=-1/ki[k1ξ1+k2ξ2+…+k(i-1)ξ(i-1)+k(i+1)ξ(i+1)+…+knξn],(1≤i≤n)。显然ξi由另外n-1个变量决定,所以自由度为n-1。
卡方分布是由正态分布构造而成的一个新的分布,对于任意正整数x, 卡方分布是一个随机变量X的机率分布。
卡方分布是指什么
卡方分布(英语:chi-square distribution[2],χ²-distribution,或写作χ²分布)是概率论与统计学中常用的一种概率分布。k个独立的标准正态分布变量的平方和服从自由度为k的卡方分布。
卡方分布是一种特殊的伽玛分布,是统计推断中应用最为广泛的概率分布之一,例如假设检验和置信区间的计算。
卡方分布在共同使用卡方检验用于拟合优度的观测分布为理论之一,独立的分类的两个标准定性数据,并在用于人口区间估计标准偏差a的来自样本标准差的正态分布。许多其他统计检验也使用这种分布,例如Friedman 的按秩方差分析。
由卡方分布延伸出来皮尔逊卡方检验常用于:
1、样本某性质的比例分布与总体理论分布的拟合优度(例如某行政机关男女比是否符合该机关所在城镇的男女比);
2、同一总体的两个随机变量是否独立(例如人的身高与交通违规的关联性);
3、二或多个总体同一属性的同素性检验(意大利面店和寿司店的营业额有没有差距)。(详见皮尔逊卡方检验)