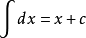反函数的导数等于直接函数导数的倒数,反函数就是将原函数中自变量与变量调换位置,用原函数的变量表示自变量而形成的函数。如:原函数是x=siny,则:反函数为y=arcsinx;反函数的导数为:(arcsin x)'=1/x'or1/(sin y)'。
反函数求导要注意什么
1、只有严格单调的可导函数,反函数才可导。事实上,不是严格单调的函数,它的反函数并不是单值映射的函数。
2、原函数的导数不等于0,否则反函数的导数没有意义。
3、一定要考虑反函数的定义域,它是原函数的值域,而不是原函数的定义域。
4、要应用定义求反函数的导函数时,一定要把原函数的解析式代入导函数中,而不是简单的更改变量的符号。这一点很多人容易忽略,所以千万要注意了。
例:求arctanx的导数:
解:y=arctanx, x∈R是x=tany, y∈(-π/2, π/2)的反函数,
因为(tany)'=(secy)^2,根据反函数的导数定义可知:
(arctanx)'=1/(tany)'=1/(secy)^2=1/(1+(tany)^2).
将x=tany代入上式,得:(arctanx)'=1/(1+x^2),x∈R.
注意到没有,在直接运用反函数的导数定义时,自变量是y,不是x,如果直接把y换成x,就会得到错误的结果。正确的做法是将原函数的解析式代入运用定义后的式子,才能转化出反函数的真正导函数。
反函数的性质有哪些
1、互为反函数的两个函数的图象关于直线y等于x对称;
2、函数存在反函数的充要条件是,函数在它的定义域上是单调的;
3、一个函数与其对应的反函数在相应区间上单调性一致;
4、偶函数一定不存在反函数,奇函数不一定存在反函数。若一个奇函数存在反函数,则反函数也是奇函数;
5、一切隐函数具有反函数;
6、一段连续的函数的单调性在对应区间内具有一致性。