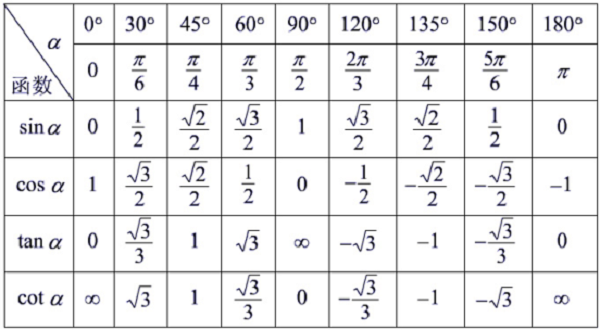
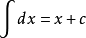相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标,是研究变量之间线性相关程度的量,一般用字母r表示。由于研究对象的不同,相关系数有多种定义方式,较为常用的是皮尔逊相关系数。
相关系数缺点
需要指出的是,相关系数有一个明显的缺点,即它接近于1的程度与数据组数n相关,这容易给人一种假象。因为,当n较小时,相关系数的波动较大,对有些样本相关系数的绝对值易接近于1;当n较大时,相关系数的绝对值容易偏小。特别是当n=2时,相关系数的绝对值总为1。因此在样本容量n较小时,我们仅凭相关系数较大就判定变量x与y之间有密切的线性关系是不妥当的。
相关系数公式
定义式
ρXY=Cov(X,Y)/√[D(X)]√[D(Y)]
公式描述:公式中Cov(X,Y)为X,Y的协方差,D(X)、D(Y)分别为X、Y的方差。
公式
若Y=a+bX,则有:
令E(X) = μ,D(X) = σ
则E(Y) = bμ + a,D(Y) = bσ
E(XY) = E(aX + bX) = aμ + b(σ + μ)
Cov(X,Y) = E(XY) − E(X)E(Y) = bσ