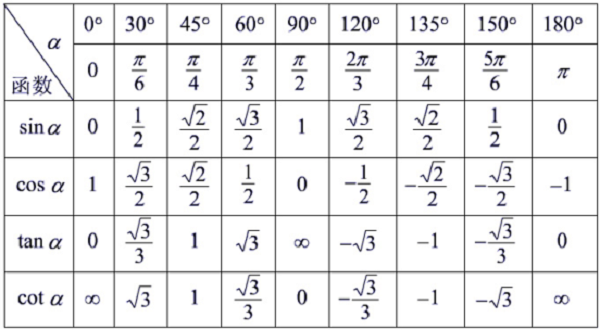
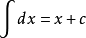两个矩阵相似的充分必要条件是:两者的秩相等;两者的行列式值相等;两者的迹数相等;两者拥有同样的特征值,尽管相应的特征向量一般不同;两者拥有同样的特征多项式;两者拥有同样的初等因子。
两矩阵相似的条件有什么
1.特征多项式相同,即|λE-A|=|λE-B|;
2.秩相同,即r(A)=r(B);
3.A,B有相同的特征值;
4.对应行列式值相同,| A|=| B|=所有特征值连乘积;
5.主对角元素和相同,即迹相同。
以上是两个矩阵相似的必要条件。
相似矩阵的定义
设A,B都是n阶矩阵,若存在可逆矩阵P,使P^(-1)AP=B,则称B是A的相似矩阵, 并称矩阵A与B相似,记为A~B。
判断两个矩阵是否相似的辅助方法:
(1)判断特征值是否相等;
(2)判断行列式是否相等;
(3)判断迹是否相等;
(4)判断秩是否相等。
以上条件可以作为判断矩阵是否相似的必要条件,而非充分条件。(两个矩阵若相似于同一对角矩阵,这两个矩阵相似。)
矩阵相似能推出什么结论
1.特征值相同
矩阵相似意味着它们具有相同的特征值。矩阵的特征值是对角线上的元素,表示矩阵在某个方向上的拉伸或收缩倍数。
如果两个矩阵相似,则它们具有相同的特征值,即它们在相同的方向上有相同的拉伸或收缩倍数。这个结论在许多数学和工程应用中都非常重要,例如线性变换和特征值分解。
2.可逆性
矩阵相似还可以推出两个矩阵之间的可逆关系。如果两个矩阵A和B相似,那么它们之间存在一个可逆矩阵P,使得P^-1*A*P=B。
这个式子可以理解为将矩阵A进行一系列相似变换后得到了矩阵B。可逆矩阵P起到了“桥梁”的作用,连接了两个相似的矩阵。这个结论在矩阵的相似变换和矩阵的可逆性的研究中有着重要的应用。