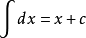如果直角三角形两直角边分别为A和B,斜边为C,那么 A²+B²=C²。直角三角形三边关系:任意两边长度之和大于第三边,任意两边之差小于第三边。具体内容小编已经整理好了,一起来看看吧。
直角三角形三边的关系是怎样的
直角三角形的三条边之间具有特定的关系,这些关系构成了直角三角形的基本性质。
首先,我们明确直角三角形的定义:一个三角形中,如果有一个角是直角(即90度),那么这个三角形就是直角三角形。在直角三角形中,最长的边称为斜边,而另外两条边则分别称为直角边。
接下来,我们探讨直角三角形三条边的数量关系。最著名的关系就是勾股定理:在直角三角形中,直角边的平方和等于斜边的平方。即,如果直角三角形的两条直角边长度分别为a和b,斜边长度为c,那么有a² + b² = c²。这个定理是直角三角形的基本性质之一,也是解决与直角三角形相关问题的关键工具。
除了勾股定理外,直角三角形三条边之间还有其他关系。例如,由于斜边是三角形中最长的边,因此它总是大于任意一条直角边。此外,根据三角形的三边关系,任意两边之和大于第三边,这一规则在直角三角形中同样适用。
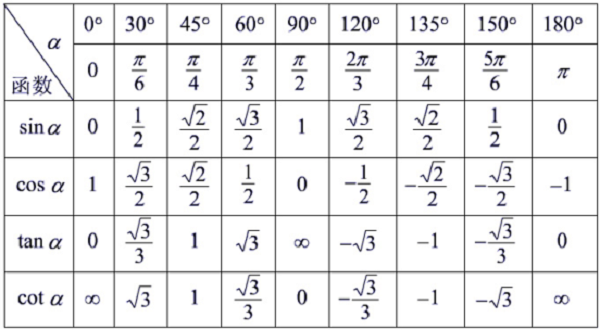
在实际应用中,我们可以利用这些关系来解决各种问题。例如,已知直角三角形的两条边,我们可以利用勾股定理求出第三条边的长度;或者,已知直角三角形的两条边和其中一个角,我们可以利用三角函数求出其他边的长度或角度。
综上所述,直角三角形的三条边之间具有多种关系,这些关系不仅有助于我们理解直角三角形的性质,还能帮助我们解决与直角三角形相关的各种问题。
直角三角形的判定方法
判定1:有一个角为90°的三角形是直角三角形。
判定2:若a^2+b^2=c^2,则以a、b、c为边的三角形是以c为斜边的直角三角形(勾股定理的逆定理)。
判定3:若一个三角形30°内角所对的边是某一边的一半,则这个三角形是以这条长边为斜边的直角三角形。
判定4:两个锐角互为余角(两角相加等于90°)的三角形是直角三角形。
判定5:若两直线相交且它们的斜率之积互为负倒数,则两直线互相垂直。那么这个三角形为直角三角形。
判定6:若在一个三角形中一边上的中线等于其所在边的一半,那么这个三角形为直角三角形。参考直角三角形斜边中线定理
判定7:一个三角形30°角所对的边等于某一邻边的一半,则这个三角形为直角三角形。