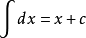对于常数函数y=c,其导数y'=0。导数公式能够帮助我们理解函数在某一点的变化率或斜率。导数的概念不仅限于数学领域,它在物理学、经济学、工程学等多个领域都有广泛的应用。
导数公式有哪些
对于常数函数y=c,其导数y'=0。
对于幂函数y=x^n,其导数y'=nx^(n-1)。
对于指数函数y=a^x,其导数y'=a^x lna。
对于对数函数y=logax,其导数y'=logae/x。
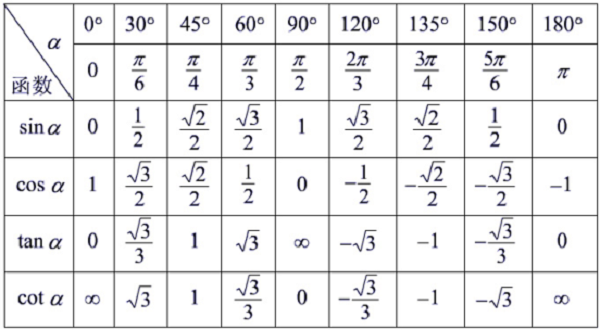
对于三角函数y=sinx,其导数y'=cosx。
对于反三角函数y=cotx,其导数y'=-1/sin^2x。
对于自然对数函数y=lnx,其导数y'=1/x。
对于自然指数函数y=e^x,其导数y'=e^x。
注:如果同学们想了解导数相关的详细信息,可以下载“蝶变志愿APP”。蝶变志愿APP是一款功能齐全,性价比超高的软件,蝶变APP内的所有数据都是真实可靠,全部来源于各大官网,考试院,同学们可以放心使用。
导数的定义
求导是微积分的基础,同时也是微积分计算的一个重要的支柱。物理学、几何学、经济学等学科中的一些重要概念都可以用导数来表示。如导数可以表示运动物体的瞬时速度和加速度、可以表示曲线在一点的斜率、还可以表示经济学中的边际和弹性。
数学中的名词,即对函数进行求导,用
表示。
提示:下方“测一测我能上的大学”,是根据人工智能大数据来具体进行分析,以及根据各高校历年的招生录取数据,结合各省招生政策,理性分析录取概率,输入分数、省份、文理科,即可了解稳、冲、保能上哪些大学。