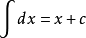等比数列求和公式:Sn=a1(1-q^n)/(1-q)(q≠1)。等差数列求和公式:Sn=na1+n(n-1)d/2。数列求和对按照一定规律排列的数进行求和。求Sn实质上是求{an}的通项公式。常见的方法有公式法、错位相减法、倒序相加法、分组法、裂项法、数学归纳法、通项化归、并项求和。
等差等比数列求和公式整理
一、等差等比数列求和公式
等差数列求和公式为:Sn=na1+n(n-1)d/2;等比数列求和公式为:Sn=a1(1-q^n)/(1-q)(q≠1)。
二、等比数列求和公式
等比数列求和公式是求等比数列之和的公式。
如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公式可以快速的计算出该数列的和。
通项公式 an=a1×q^(n-1)
求和公式 a1(1-q^n)/(1-q)
Sn=a1(1-q^n)/(1-q)(q≠1)
求和公式推导
(1)Sn=a1+a2+a3+.+an(公比为q)
(2)qSn=a1q + a2q + a3q +.+ anq = a2+ a3+ a4+.+ an+ a(n+1)
(3)Sn-qSn=(1-q)Sn=a1-a(n+1)
(4)a(n+1)=a1q^n
(5)Sn=a1(1-qn)/(1-q)(q≠1)
三、等差数列求和公式
等差数列是常见数列的一种,可以用AP表示,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列,而这个常数叫做等差数列的公差,公差常用字母d表示。例如:1.3.5.7.9……(2n-1)。等差数列{an}的通项公式为:an=a1+(n-1)d。前n项和公式为:Sn=n*a1+n(n-1)d/2或Sn=n(a1+an)/2。注意: 以上整数。
Sn=n(a1+an)/2
Sn=na1+n(n-1)d/2=dn^2/2+(a1-d/2)n
末项=首项+(项数-1)×公差
项数=(末项-首项)÷公差+1
首项=末项-(项数-1)×公差
和=(首项+末项)×项数÷2
末项:最后一位数
首项:第一位数
项数:一共有几位数
和:求一共数的总和
常见求和公式整理
等差数列求和公式
等差数列求和公式为:
[ S_n = \frac{n(a_1 + a_n)}{2} ]
或者
[ S_n = \frac{n}{2} [2a_1 + (n - 1)d] ]
其中,( a_1 ) 是首项,( a_n ) 是第n项,( d ) 是公差,( n ) 是项数。
Excel中的常见求和公式
普通求和:选中求和区域的行和列,使用快捷键Alt+=即可获得求和结果。
区域求和:使用SUM函数,例如=SUM(B2:D2)。
指定区域求和:使用SUM函数,例如=SUM(B3:B4, B7:B8)。
多区域求和:使用SUM函数,例如=SUMIF(B2:D2,"业绩")。
合并单元格求和:使用SUM函数,例如=SUM(C2:C11)-SUM(D3:D11)。
隔列求和:使用SUMIF函数,例如=SUMIF($B$2:$E$2,F$2,$B3:$E3)。
乘积求和:使用SUMPRODUCT函数,例如=SUMPRODUCT(B2:B11, C2:C11)。
其他常见求和公式
错位相减法:适用于等差数列与等比数列的乘积。
阿贝尔求和公式:适用于特定类型的数列求和。
倒序相加法:适用于某些特定的数列求和问题。
分组法:将数列分组后进行求和。
裂项相消法:通过裂项后相消进行求和。
数学归纳法:通过归纳法推导数列的求和公式。
通项化归法:将通项公式化归为易于求和的形式。
并项求和法:将数列并项后进行求和。