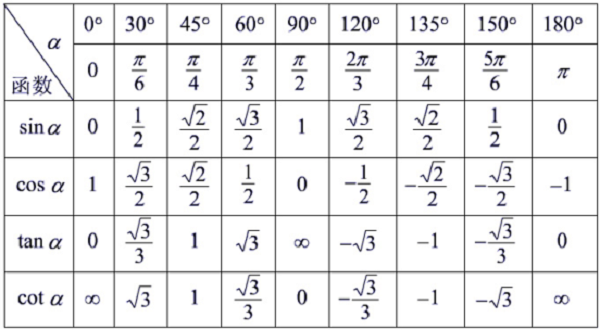
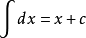导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f’(x0)或df(x0)/dx。
导数的基本公式是什么
y=c(c为常数) y'=0;
y=x^n y'=nx^(n-1);
y=a^x y'=a^xlna y=e^x y'=e^x;
y=logax y'=logae/x y=lnx y'=1/x ;
y=sinx y'=cosx ;y=cosx y'=-sinx ;
y=tanx y'=1/cos^2x ;
y=cotx y'=-1/sin^2x。
温馨提示:想查看更多导数的基本公式,可以下载《蝶变志愿》APP,APP内了解更多院校信息,包括历年的院校和专业分数线、院校综合排名、优势学科、院校就业情况等信息都可查询。
导数的运算法则是什么
加(减)法则:[f(x)+g(x)]'=f(x)'+g(x)'
乘法法则:[f(x)*g(x)]'=f(x)'*g(x)+g(x)'*f(x)
除法法则:[f(x)/g(x)]'=[f(x)'*g(x)-g(x)'*f(x)]/g(x)^2
要注意的是不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。反之,已知导函数也可以反过来求原来的函数,即不定积分。
提示:下方“测一测我能上的大学”,是根据人工智能大数据来具体进行分析,以及根据各高校历年的招生录取数据,结合各省招生政策,理性分析录取概率,输入分数、省份、文理科,即可了解稳、冲、保能上哪些大学。