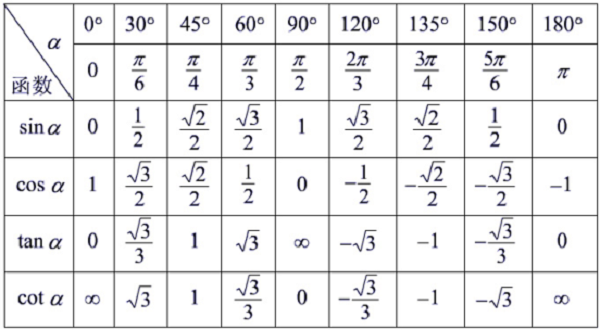
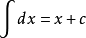极限是微积分中的基础概念,它指的是变量在一定的变化过程中,从总的来说逐渐稳定的这样一种变化趋势以及所趋向的值(极限值)。在现代的数学分析教科书中,几乎所有基本概念(连续、微分、积分)都是建立在极限概念的基础之上。(文章内容来源于网络,仅供参考)
重要极限的公式是什么
两个重要极限公式:第一个重要极限公式是:lim((sinx)/x)=1(x->0),第二个重要极限公式是:lim(1+(1/x))^x=e(x→∞)。
对于被考察的未知量,先设法正确地构思一个与它的变化有关的另外一个变量,确认此变量通过无限变化过程的’影响‘趋势性结果就是非常精密的约等于所求的未知量;用极限原理就可以计算得到被考察的未知量的结果。
两个重要极限的具体内涵
重要极限是x趋向于∞不是趋向于+∞,右面不能相等因为不符合重要极限的定义。数学中的“极限”指:某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中。
逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”的过程中,此变量的变化,被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。
极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”(当然也可以用其他符号表示)。
极限四则运算法则
极限的四则运算法则是:当数列{an},{bn}分别以a,b为极限时,数列{an±bn}的极限是a±b,
数列{anbn}的极限是ab;当bbn不等于0时,{an/bn}的极限是a/b. 当函数f,g分别以a,b为极限时,函数f±b的极限是a±b,
函数fg的极限是ab;当bg不等于0时,{f/g}的极限是a/b。
可见,虽然极限分为函数极限和数列极限,不过它们的四则运算法则是一模一样的。
极限的性质
1、唯一性:若数列的极限存在,则极限值是唯一的,且它的任何子列的极限与原数列的相等。
2、有界性:如果一个数列’收敛‘(有极限),那么这个数列一定有界。
但是,如果一个数列有界,这个数列未必收敛。例如数列 :“1,-1,1,-1,……,(-1)n+1”
3、保不等式性:设数列{xn} 与{yn}均收敛。若存在正数N,使得当n>N时有xn≥yn,则(若条件换为xn>yn,结论不变)。