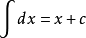高中数学公式大全及高考常用公式汇总

公式大全

相关标签：二元一次方程

x的a次方的导数
x的a次方的导数是ax^a-1。x^a求导等于a*x^(a-1)。解:令y=x^a，那么当a=0时，则y=x^0=1，则y=0，当a≠0时，则y=(x^a)=a*x^(a-1)，即x^a的导数为a*x^(a-1)。x的a次方的导数是多少x的a次方的导数是指数的导数，x^a的导数[详细]
2023-05-16 18:19分类：公式大全
矩阵的行秩和列秩一定相等吗
矩阵的行秩和列秩，二者一定是相等的。行秩和列秩通过进行计算之后得到的都是矩阵的秩，这是秩的基本性质和定理。在线性代数中，一个矩阵A的列秩是A的线性独立的纵列的极大数目。类似地，行秩是A的线性无关的横行的极[详细]
2023-05-16 18:19分类：公式大全
矩阵的乘法运算法则
矩阵的乘法运算法则有：乘法结合律：（AB）C=A（BC）；乘法左分配律：（A+B）C=AC+BC；乘法右分配律：C（A+B）=CA+CB；对数乘的结合性k（AB）=（kA）B=A（kB）。矩阵乘法的定义与性质定义：[详细]
2023-05-16 18:14分类：公式大全
幂函数导数
幂函数求导公式：y\'=ay/x=ax^a/x=ax^(a-1)。幂函数导数公式的证明：y=x^a，两边取对数lny=alnx，两边对x求导（1/y)*y\'=a/x，所以y\'=ay/x=ax^a/x=ax^(a-1)。幂函数求导公式幂函数导数公式的证明：[详细]
2023-05-16 18:14分类：公式大全
线性插值法
插值法又称“内插法”，主要包括线性插值、抛物线插值和拉格朗日插值等。其中的线性插值法是指使用连接两个已知量的直线，来确定在这两个已知量之间的一个未知量的值。线性插值法是什么意思线性插值是指插值函数为一[详细]
2023-05-16 13:28分类：公式大全
导数的基本公式
导数的计算公式为：y=c(c为常数)y\'=0；y=x^ny\'\"=nx^(n-1)；y=a^xy\'=a^xIna，y=e^xy\'=e^x；y=logaxy\'=logae/x，y=Inxy\'=1/x。导数的基本公式是什么导数的基本公式：y=c(c为常数) y\'=0、y=x^n y\'=nx^(n-1) 。[详细]
2023-05-13 17:01分类：公式大全
cosx的平方的导数
cosx平方的导数是-2sinxcosx。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线[详细]
2023-05-13 16:56分类：公式大全
y=ln(2x+1)的导数
y=ln(2x+1)的导数是2/(2x+1)。解析如下：y\'=1/(2x-1) *（2x-1)的物罩导数=2/(2x-1)，补充：这是复合函数的求导,（2x-1)的导数为2。y\'=1/(2x-1) *（2x-1)的导数等于2/(2x-1)。y=ln(2x+1)的导数y=ln[1/(2x+1)]y‘=(2[详细]
2023-05-13 15:15分类：公式大全
副对角线矩阵的逆矩阵公式
副对角线矩阵的逆矩阵公式：AA-1=A-1A=E。对角矩阵可以认为是矩阵中最简单的一种，值得一提的是：对角线上的元素可以为0或其他值，对角线上元素相等的对角矩阵称为数量矩阵;对角线上元素全为1的对角矩阵称为单位矩阵[详细]
2023-05-11 10:24分类：公式大全
求极限lim的常用公式
求极限lim的常用公式：①lim(f(x)+g(x))=limf(x)+limg(x)；②lim(f(x)-g(x))=limf(x)-limg(x)；③lim(f(x)*g(x))=limf(x)*limg(x)。极限lim的常用公式1、lim（f（x）+g（x））=limf（x）+limg（x）；[详细]
2023-04-23 14:31分类：公式大全
可逆矩阵的行列式
可逆矩阵与其逆矩阵是大学数学（高数）中的重点知识也是期末考试和研究生入学考试中的高频考点。本文重点来谈谈“逆矩阵的行列式值与原矩阵行列式的关系”：逆矩阵的行列式与原矩阵的行列式的乘积为1，即二者互为倒数[详细]
2023-04-18 12:24分类：公式大全
a的伴随矩阵的伴随矩阵等于什么
a的伴随矩阵的伴随矩阵等于a的逆矩阵。等于A的行列式的n-2次方再乘以A，可以有概念推导出来。a的伴随矩阵的伴随矩阵是什么不需要A一定是可逆.[详细]
2023-04-15 09:42分类：公式大全